About
Networks provide an efficient formalism to study many complex real-world systems. They provide a natural modeling framework of structural and functional brain networks, protein interaction networks, social interactions, information and epidemic spreading, and infrastructural and financial networks. Real-world networks and dynamic processes that take place in them show heterogeneous, non-Markovian, and intrinsically correlated topologies and dynamics, making their analysis particularly challenging.
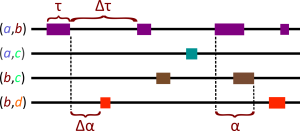
This project aims at developing versatile, robust, and scalable numerical and statistical methods for the analysis of empirical networks and dynamical processes that take place in them. We have recently developed a general and consistent framework for numerically generated randomized reference (null) models (RRMs) for networks, in particular networks with a time-evolving topology, providing procedures for generating, applying and interpreting RRMs for empirical networked systems (paper). Current work focuses on applying this framework to uncover and characterize computational motifs in the microcircuitry of the Drosophila larva brain (project webpage).
Past work has focused on the development of fast, Gillespie-type algorithms for simulating stochastic processes on networks (open access textbook, and paper and python library for simulations on temporal networks) and on methods for correcting biases due to incomplete sampling of empirical networks (paper).