Présentation
This project aims to characterize the mircrociruit structure of small animals’ brains and link this to how the brain processes information and encodes behavior. The project relies on simultaneous access to recent synapse-resolution wiring diagrams of complete brain regions and single-neuron optogenetic control in freely behaving animals. We employ methods from graph theory, statistical learning, and information theory to characterize the topology and structure of microcircuits in animal brains and to link the circuits’ structures to how they perform decision making and generate behavioral sequences.
A prominent hypothesis for how the brain’s wiring is organized is that it is made up of stereotyped “canonical” microcircuits. Relying on a restricted set of repeated circuits, optimized for specific functions, may provide biologically advantageous inductive biases for efficient learning and help encode innate behaviors. Information theory furthermore tells us that the presence of statistically regular circuits makes the connectome compressible. Canonical microcircuits thus provide a means that evolution may have selected to encode the neural wiring information more efficiently in the limited storage space of the genome.
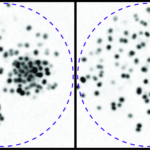
Extracting the statistical regularities (“motifs”) of a connectome is a challenging inverse problem since one often has access to only a single experimental realization (i.e., a single graph). The analysis necessarily relies on a statistical “null” model against which statistical significance is defined. The choice of this null model is ambiguous however, leading to possible uncontrolled biases (Fig. 1A). We developed an approach to mining significant graph features which applies a hierarchy (arxiv.org/abs/1806.?????) of increasingly constrained microcanonical random graph models. This allows us to conservatively infer significant features in a manner that is less sensitive to null model choice and filter out spurious motifs that can simply be explained as statistical consequences of these (Fig. 1B).