Presentations
I am a theoretical physicist working at the frontier of statistical physics and computational biology. I combine analytical and numerical approaches to understand biological systems using physico-mathematical models. I initially explored random walk theory, studying first-passage events for random walks characterized by long-term memory. Then, I moved on to decision-making theory inspired by physics-based principles, such as the information maximization principle, and applied these to multi-armed bandit systems. Now, I’m focused on how these decision strategies are encoded in small neural circuits such as in Drosophila larvae, aiming to uncover the biological properties of decision-making shaped by embodiment.
PhD research
My PhD work focused on complex random walks with long range memory effects with the goal to provide new frameworks to model and understand the random walks of biomolecules, chemical reactions and animal taxis. I had two major topics: 1) first passage problems for non-Markovian random walkers and 2) characterizing the properties of self-reinforced random walks.
The first passage time (FPT), defined as the time needed for a random walker to reach a given target point, is a key quantity for characterizing dynamic processes in a wealth of real-world systems (transport-limited reactions, neuron firing dynamics). I studied strongly non-Markovian random walks (whose dynamics depend on their entire history) as a proxy to model complex environments. Among them, self-reinforced random walks (SRRWs) are a class of random walks where memory effects emerge from the interaction of the random walker with the territory that it has visited at earlier times. They are often used to model complex processes in ecology, epidemiology and computer science and are notoriously difficult to characterize.

Figure: Kymograph of an MDCK epithelial cell, whose trajectory exhibits oscillations. The cell appears to change direction when it reaches the edges of the previously visited territory, highlighting the coupling between the explored territory and the future dynamics of the trajectory. The visited territory slowly expands over time, allowing the oscillations to increase in amplitude, a typical behavior of self-reinforced random walks. Image taken from: [d’Allesandro et al. 2021, Nature Communications].
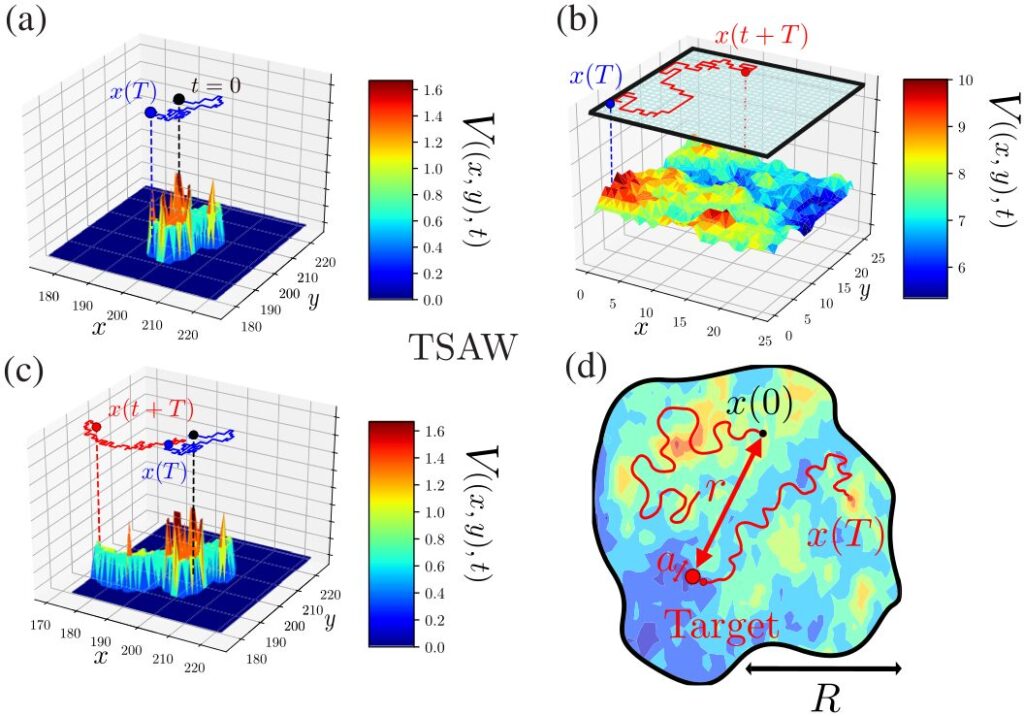
Figure: Examples of 2D reinforcement trajectories (TSAW model): In panel (a), the random path from t=0 to T generates the local energy landscape V(x,y,t) [proportional to the total number of visits at (x,y) up to t], represented along the vertical axis z. This dynamic leads to long-term memory effects and aging across all timescales. The trajectory after T, shown in panel (c), explicitly depends on the entire territory visited by the walker up to T. The visit statistics of each site are radically altered by the introduction of confinement (b). Therefore, the dynamics of reinforcement random walks depend on the geometry of the space in which they evolve. Panel (d) highlights the main objectives of my work, namely to quantify the exploration properties (first-passage time and geometry) of self-reinforced random walks in confined space. Image taken from: [Alex et al., 2022, Physical Review X].
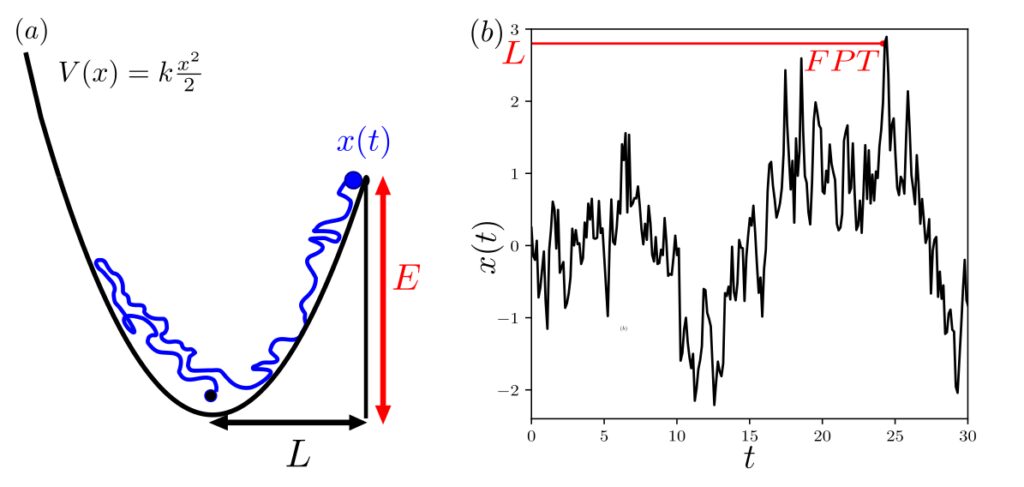
Figure: (a) Let x(t) be a random walker in a harmonic potential at a given temperature, subject to a friction kernel that asymptotically follows a power law. The friction then generates long-term memory effects (⟨x(t)x(t′)⟩ decays according to a power law). The goal is to determine the mean first-passage time (FPT) to a target located at x=L which can only be reached by overcoming an energy barrier E=V(L)−V(0). (b) Schematic of the first-passage time (FPT) for a single stochastic trajectory of x(t) described in (a). Image taken from: [Alex et al., 2024, Nature Communications]
Past postdoctoral research
From local memory-based decisions without cognition, my interest shifted towards developing new generic frameworks to model and understand cognitive decision-making. An essential point for me is to develop such decision frameworks while providing analytical mathematical solutions avoiding current trends in accepting black box solutions such as the ones often provided in machine learning.
I chose the multi-armed bandit (MAB) problem as a general formalism because this mathematical problem embodies the issues of exploration and exploitation tradeoff. The MAB model is a simple slot machine game where the goal is to maximize the payout by finding and playing the best arms. Since pulling sub-optimal solutions is costly, MAB algorithms must carefully quantify their exploration time and have to be robust to noisy inputs. As a direct consequence, this abstract framework finds application across a wide spectrum of domains, comprising neuroscience, reinforcement learning, and pharmaceutical trials.
I developed a new approach derived from physical principles, by optimizing a functional over the global bandit games, enabling its extension beyond its usual scopes.
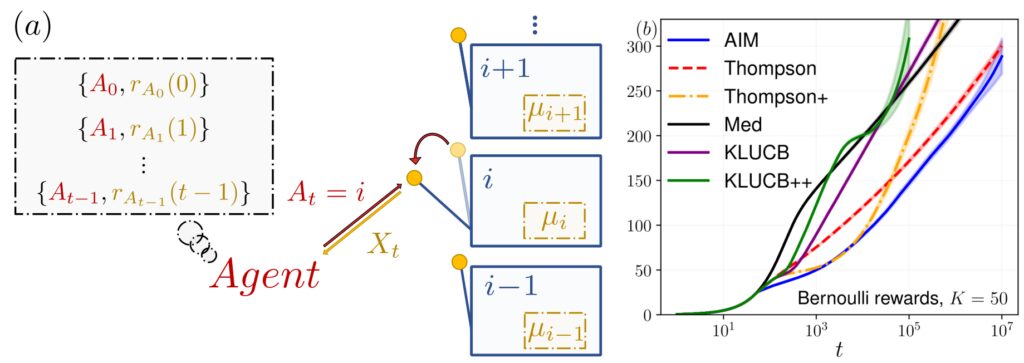
Figure: (a) Illustration of the multi-armed bandit problem. At each time step t, the agent selects an action At that returns a reward r(t), drawn from a distribution with an unknown mean μi. The agent’s goal is to minimize the cumulative regret measured relative to the optimal choice (in this case, the arm with the highest mean). (b) Evolution of the Bayesian regret for a 50-armed bandit with Bernoulli rewards, with means drawn from a uniform distribution. Our algorithm is represented in blue. Image taken from: [Alex et al., 2024, Physical Review E].
Recently, I have focused on obtaining low-dimensional latent spaces that fully characterize the connectivity of invertebrate brains, known as connectomes, at the scale of individual neurons and synapses. Since connectome data are often high-dimensional, it is challenging to identify neural circuit structures and their functions through an exhaustive screening of an entire connectome. Therefore, it is crucial to extract relevant low-dimensional representations. We have developed an approach to generate a latent space specifically designed to model the structural and functional constraints of neural connectomes. Our model represents synaptic connections between each pair of neurons using a dual-space framework with learnable distance kernels.
Our approach allows us to: 1) extract a low-dimensional latent representation of a connectome; 2) account for synaptic weights and asymmetries in connectivity by using two distinct spaces for afferent and efferent connections; 3) learn the most suitable distance kernels and the most efficient latent space dimension to characterize the connectivity matrix; 4) identify specific features in the latent space to uncover hidden structural details; 5) generate artificial connectomes with realistic structural properties.
Our approach has been applied to synthetic connectome models and the complete connectome of adult Drosophila melanogaster.
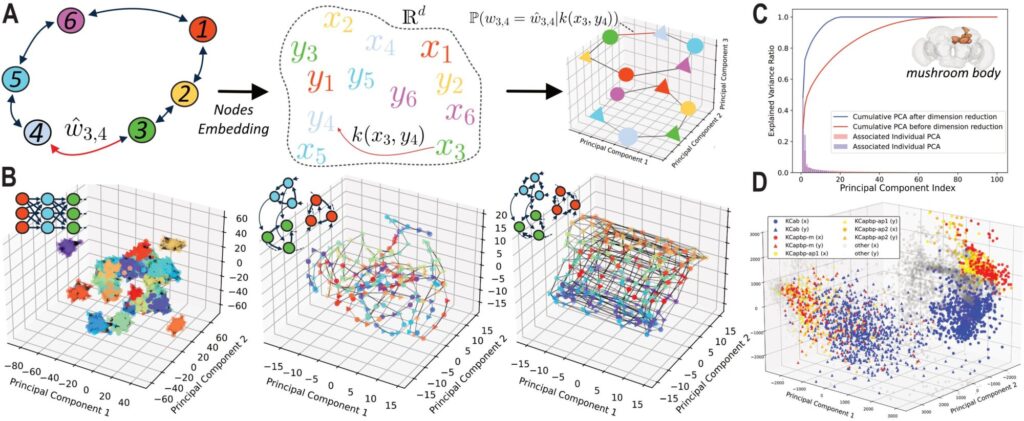
Figure: (a) Schematic overview of our approach. (b) Application to artificial structures. (c-d) Application to a brain region of adult Drosophila melanogaster a) We use a dual latent space in dimension ddd, representing pre- and post-synaptic connections. The connection probability and weight are modeled through a parametric generative function based on a non-Euclidean distance kernel k(xi,yj)k(x_i, y_j)k(xi,yj) between pairs in the latent space. The model is trained by maximizing the log-likelihood of the observed connectome matrix using an underlying Bayesian generative model (synaptic weights between pairs of neurons). b) 3D projection of the principal components of the trained latent space for a synfire chain, an asymmetric torus (non-reciprocal connections), and a bidirectional torus, from left to right. The latent space successfully captures the latent structure of the synthetic connectomes as well as their relative weights. c) Explained variance ratio across successive principal components of the embedding associated with a region of an adult Drosophila melanogaster connectome. Before dimensionality reduction (red), the latent space is situated in a high-dimensional space. Dimensionality reduction is then performed via nuclear norm regularization. The prediction performance of the embedding space is evaluated using a link prediction method, which optimizes both regularization and dimensionality. The final latent space converges to a low-dimensional representation. d) 3D PCA projection of the final embedding. Four cell types identified in the FlyWire connectome codex form distinct clusters, demonstrating the approach’s ability to reveal hidden biological properties.

Figure: Segmentation of the muscles of a Drosophila larva obtained from a CT scan of a Drosophila melanogaster larva. To accurately model the locomotor system and its interaction with the nervous system, we are developing a numerical simulation tool. This tool is based on the body and muscle geometry shown above and simulates muscle and mechanical dynamics using finite elements, a Hill model for muscle actuation, and contact dynamics with friction, enabling the reproduction of various observed motor patterns.

