Présentations
Je suis un physicien théoricien travaillant à la frontière de la physique statistique et de la biologie computationnelle. Je combine des approches analytiques et numériques afin d’étudier les systèmes biologiques par des modèles physico-mathématiques. Mes premiers travaux ont porté sur la théorie des marches aléatoires, en particulier les événements de premier passage pour des marches aléatoires caractérisées par des effets de mémoire à long terme. Par la suite, j’ai exploré la théorie de la prise de décision, en m’inspirant de principes physiques comme le principe de maximisation de l’information, que j’ai appliqués aux systèmes de bandits manchots. Désormais, je m’intéresse aux principes régissant l’implémentation des stratégies de décision dans de petits circuits neuronaux, comme ceux observés chez les larves de Drosophila. Mon objectif est d’étudier dans quelle mesure les structures de ces circuits biologiques sont influencées par les contraintes imposées par l’environnement et la réalité biologique des circuits.
Doctorat
Mes travaux de doctorat se sont essentiellement concentrés sur l’étude de marches aléatoires complexes qui présentent des effets de mémoire à longue portée, et cela afin de fournir de nouveaux cadres de modélisation de marches aléatoires qui sont obsérvées pour des biomolécules, des réactions chimiques et mouvements d’animaux. Mes travaux se présentent selon deux axes principaux : 1) les problèmes de première passage pour les marcheurs aléatoires non-markoviens et 2) la caractérisation des propriétés des marches aléatoires à renforcement.
Le temps de premier passage (FPT en anglais), défini comme le temps nécessaire pour qu’un marcheur aléatoire atteigne un point cible donné, est une quantité clé pour caractériser les processus dynamiques dans une multitude de systèmes réels (réactions limitées par le transport, dynamiques des neurones). Mon intérêt s’est porté sur l’étude des marches aléatoires fortement non-markoviennes (dont la dynamique dépend de leur histoire complet) utilisées comme un proxy pour modéliser des environnements complexes. Parmi elles, les marches aléatoires à renforcement sont une classe de marches aléatoires où les effets de mémoire émergent de l’interaction du marcheur aléatoire avec le territoire qu’il a précédemment visité. Elles sont souvent utilisées pour modéliser des processus complexes en écologie, épidémiologie et informatique et sont notoirement difficiles à caractériser.

Figure : Kymographe d’une cellule épithéliale MDCK, dont la trajectoire exhibe des oscillations. La cellule semble changer de direction lorsqu’elle atteint les bords du territoire précédemment visité, soulignant le couplage entre le territoire précédemment exploré et la dynamique future de la trajectoire. Le territoire visité s’étend lentement au fil du temps, permettant aux oscillations d’augmenter en amplitude, un comportement typique des marches aléatoires avec renforcement. Image tirée de [d’Allesandro et al. 2021, Nat Comm]
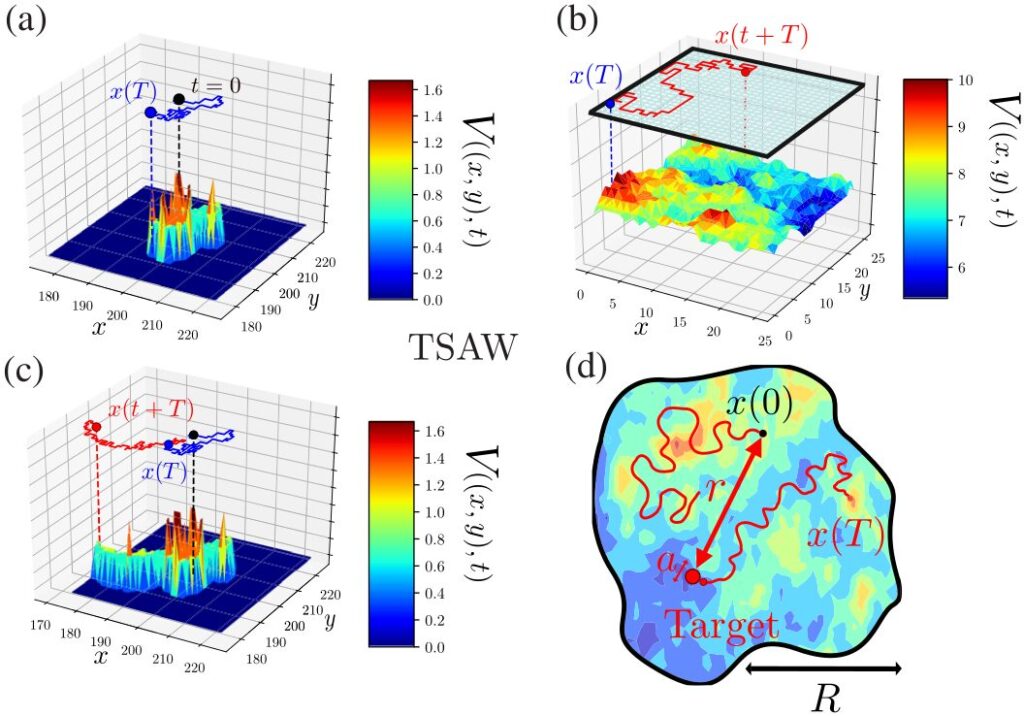
Figure: Exemples de trajectoires à renforcement en 2D (modèle TSAW) : Dans le panneau (a), le chemin aléatoire de t = 0 à T génère le paysage énergétique local V(x, y,t) [proportionnel au nombre total de visites en (x,y) jusqu’à t], représenté le long de l’axe vertical z. Cette dynamique entraîne des effets de mémoire à long terme et un vieillissement à toutes les échelles de temps. La trajectoire après T, représentée dans le panneau (c), dépend explicitement de l’ensemble du territoire visité par le marcheur jusqu’à T. Les statistiques des visites de chaque site sont radicalement modifiées par l’introduction d’un confinement (b). La dynamique des marches aléatoires à renforcement dépend donc de la géométrie de l’espace dans lequel elles évoluent. Le panneau (d) souligne les objectifs principaux de mes travaux, à savoir quantifier les propriétés d’exploration (temps de premier passage et géométrie) des marches aléatoires à renforcement en espace confiné. Image tirée de [Alex et al, 2022, Phys. Rev. X]
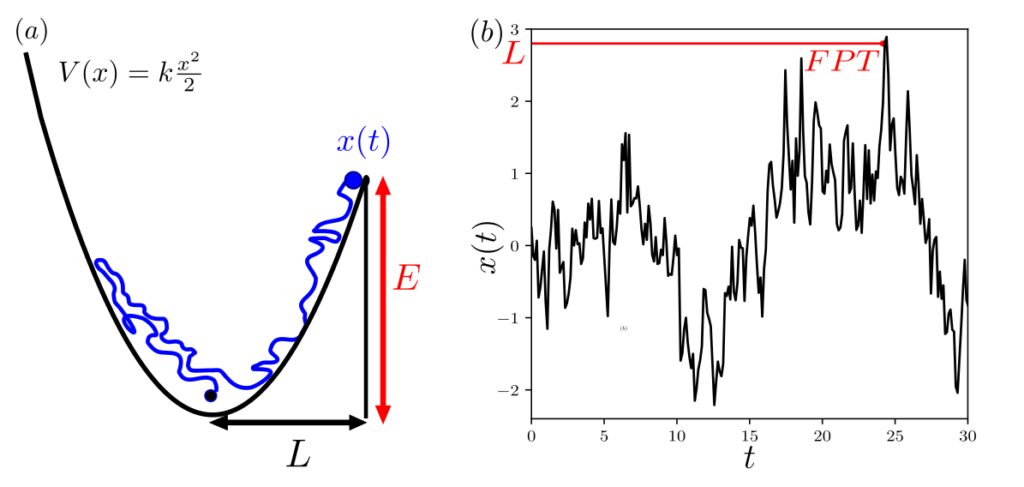
Figure: a. Soit x(t) un marcheur aléatoire dans un potentiel harmonique à une température donnée, soumis à un noyau de friction suivant asymptotiquement une loi de puissance. La friction génére alors des effets de mémoire à long terme (<x(t)x(t’>) décroît selon une loi de puissance). On cherche alors à déterminer le temps moyen de premier passage (FPT) d’une une cible située en x=L, qui ne peut être atteinte qu’en surmontant une barrière d’énergie E=V(L)−V(0). b. Schéma du temps de premier passage (FPT) pour une trajectoire stochastique unique de x(t) vérifiant (a). Image tirée de [Alex et al, 2024, Nat Comm]
Postdoctorat
De décisions basées sur la mémoire locale sans cognition, mon intérêt s’est déplacé vers le développement de nouveaux cadres génériques pour modéliser et comprendre la prise de décision cognitive. Un point essentiel pour moi est de développer de tels cadres décisionnels tout en fournissant des solutions mathématiques analytiques à l’opposé de solutions non analytiquement tractables telles que celles souvent fournies dans l’apprentissage automatique.
En particulier, je me suis intéressé au problème du bandit manchot (MAB), qui présente un formalisme incarnant les problèmes génériques de compromis entre exploration et exploitation. Le modèle MAB est un simple jeu de machine à sous où l’objectif est de maximiser ses gains en trouvant puis en jouant les meilleures solutions. Puisque tirer des solutions sous-optimales est coûteux, les algorithmes MAB doivent apprendre à quantifier avec soin leur temps d’exploration et doivent être robustes aux perturbations. En conséquence, ce cadre abstrait trouve des applications dans un large spectre de domaines, comme les neurosciences, l’apprentissage par renforcement et les essais pharmaceutiques.
Au cours de mon postodoctorat, j’ai notemmant développé une nouvelle approche dérivée de principes physiques, qui en optimisant une fonctionnelle sur les jeux de bandit, permet d’étendre son application au-delà de ses domaines d’utilisation traditionnels.
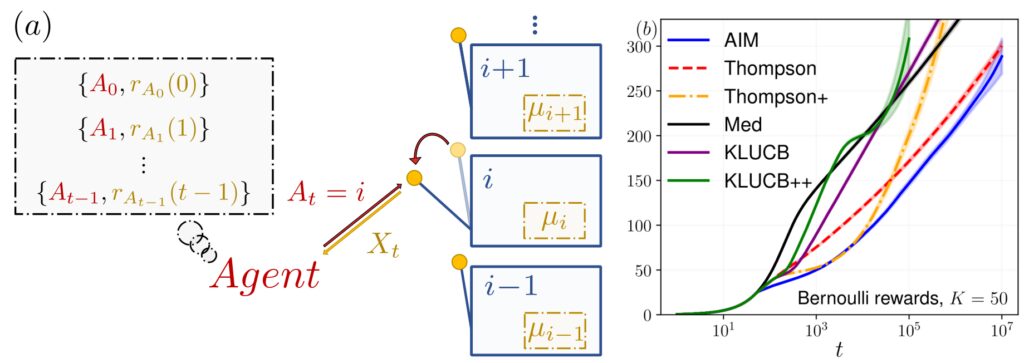
Figure: a) llustration du problème du bandit à plusieurs bras. À chaque instant t l’agent tire une action At en qui renvoie une récompense r(t), tirée d’une distribution de moyenne inconnue μi. L’objectif de l’agent est de minimiser le regret cumulatif mesuré par rapport au choix optimal (ici le bras avec la meilleur moyenne). (b) Évolution du regret bayésien pour un bandit à 50 bras avec des récompenses suivant une loi de Bernoulli, les moyennes étant tirées selon sune loi uniforme. Notre algorithme est représenté en bleu. Image tirée de [Alex et al, 2024 Phys. Rev. E].
Récemment, je me suis tourné vers l’obtention d’espace latent en basse dimesnion caractérisant intégralement la connectivité des cerveaux des invertébrés, appelés connectomes, à l’échelle des neurones individuels et des synapses. Comme ses données de connectome sont souvent en haute dimension, il difficile d’identifier des structures des circuits neuronaux ainsi que leur fonction par un criblage exhaustif de l’ensemble d’un connectome. Ainsi, il est essentiel d’extraire des représentations pertinentes en basse dimension. Ainsi, nous avons dévelloper une approche de génération d’espace latent spécifiquement conçue pour modéliser les contraintes structurelles et fonctionnelles des connectomes neuronaux. Notre modèle permet de représenter les connexions synaptiques entre chaque paire de neurones, basée espace dual et des noyaux de distance apprenables. Notre approche permet de 1) extraire une représentation latente en basse dimension d’un connectome ; 2) tenir compte des poids synaptiques et des asymétries dans la connectivité en utilisant deux espaces distincts pour les connexions afférentes et efférentes; 3) apprendre les noyaux de distance les plus appropriés ainsi que la dimension de l’espace latent la plus efficace pour caratériser la matrice de connectivité; 4) Identifier des caractéristiques spécifiques dans l’espace latent pour révéler des particularités structurelles cachées ; 5) générer des connectomes artificiels avec des caractéristiques structurelles réalistes. Notre approcha a été appliquée sur des modèles de connectomes synthétiques et sur le connectome complet de l’adulteDrosophila melanogaster.
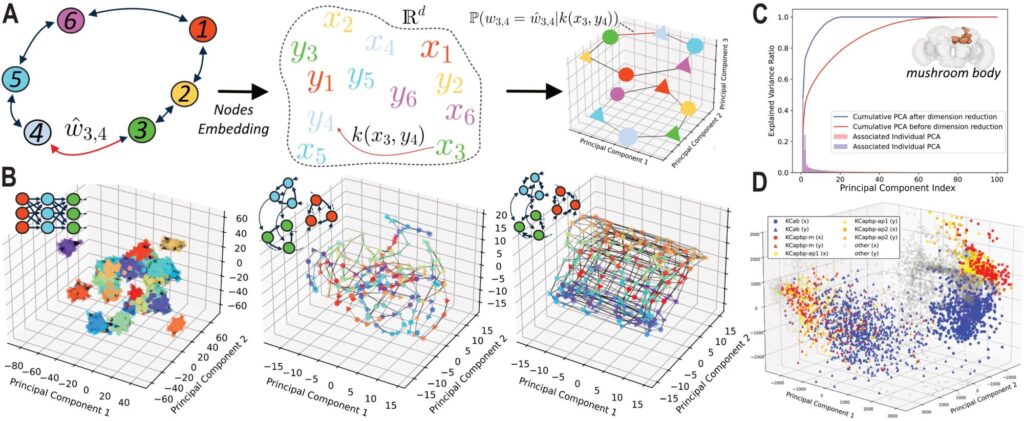
Figure: a) Vue schématique de notre approche. b) Application à des structures artificielles.c-d) Application à une région du cerveau de l’adulte de la Drosophila melanogaster. a) Nous utilisons un double espace latent en dimension d), représentant les connexions pré- et post-synaptiques. La probabilité de connexion et le poids sont modélisés via une fonction générative paramétrique basée sur un noyau de distance non-euclidien k(xi,yj) entre des paires de l’espace latent. Le modèle est entraîné en maximisant la log-vraisemblance de la matrice de connectome observée selon un modèle gnératif Bayesien sous-jacent (poids synaptiques entre paires de neurones). b) Projection 3D des composantes principales de l’espace latent entraîné pour une chaîne synfire, un tore asymétrique (connexions non réciproques) et un tore bidirectionnel, de gauche à droite. L’espace latent capture avec succès la structure latente des connectomes synthétiques ainsi que leurs poids relatifs. c) Ratio de variance expliquée par les composantes principales successives de l’embedding associé pour une région d’un connectome de l’adulte de la Drosophila melanogaster. Avant la réduction de dimension (rouge), l’espace latent est compris dans un espace de haute dimension. La réduction de dimension est ensuite réalisée via une régularisation de norme nucléaire. La performance de prédiction de l’espace d’embedding est mesurée via une méthode de prédiction des liens, ce qui permet d’optimiser la régularisation et la dimensionnalité. L’espace latent final converge vers un espace de basse dimension. c) Projection 3D par PCA de l’embedding final. Quatre types cellulaires identifiés dans le codex du connectome FlyWire forment des clusters distincts, démontrant la capacité de l’approche à révéler des propriétés biologiques cachées.

Figure: Segmentation des muscles d’une larve de Drosophile obtenu à partir d’un CT scan d’une larve de Drosophila melanogaster. Pour modéliser avec précision le système locomoteur et son interaction avec le système nerveux, nous développons un outil de simulation numérique. Celui-ci se base sur la géométrie corporelle et musculaire ci-dessus, et simule les dynamiques musculaires et mécaniques via des éléments finis, un modèle de Hill pour les muscles, et la dynamique de contact avec friction, permettant de reproduire divers schémas moteurs observés.

